The Jarno Taper

1. Description

1.1. Rate of Taper

The Jarno taper has the same rate of taper in all sizes. That is to say, if you think of an indefinitely long cone with this taper, each individually numbered Jarno taper is just a section of this one cone.

The rate of taper itself is 1 in 20 measured diametrically. That is, for every 20 units you go along the cone, it gets 1 unit wider in diameter.

When measuring in inches, this would mean that for every 20 inches of the cone, it would increase in diameter by 1 inch. It is more convenient to do it the other way around: for every 1 inch of length, the cone increases 1/20 inches (0.05 inches) in diameter.

(I don't think it makes any particular sense to bring feet into this, since you never deal with Jarno tapers that are multiple feet long. Still, for reasons unknown to me, this taper is usually expressed as an increase in diameter (in inches) per foot of length. Since a foot is 12 inches, the taper per foot, in inches, is 0.05 * 12 = 0.6. "Jarno" (Oscar J. Beale) did not so express it when he introduced the taper; he used inches-per-inch. This seems a far better way to express it, because the rate of taper is really a dimensionless unit: 0.05.)

To express this rate of taper in degrees, take the inverse tangent (arc tan) of the diametrical increase divided by the longitudinal increase ("rise / run"). Thus arctan(1/20) = arctan(0.05) = 2.864 degrees included angle, approximately.

1.2. Defining Specific Taper Sections

With a taper such as the Morse, where the rate of taper of every numbered taper is different, establishing a particular numbered taper is ad hoc. You must look the taper up in a table, because it conforms to no system or principle.

With a taper with a constant rate of taper, such as the Jarno, establishing specific tapers within it is just a matter of adopting some convenient scheme for cutting the cone which contains all of the tapers into sections.

Slice the 1:20 tapering cone at any given point and take this as the diameter of the small end of a finite taper section. Let's say that I want to make the big end 25 percent larger than the small end. Because the taper is 1-in-20 I need to go 5 times the small-end diameter down the taper to get to the big-end diameter. (That is, for every small-end diameter I go along the taper, it gets 0.05 times that diameter larger. 0.05 * 5 = 0.25 = 25 percent larger.)

So far, this seems rather arbitary. But if one converts it all into fractions, a lovely system emerges.

Let's say that the small end, whatever it is, is N tenths of some unit. The number N is itself dimensionless, and the units may be in any system you wish (though once you pick a unit you must stick with it).

(The Jarno system was defined in inches, so typically this would be N tenths of an inch. It would work in any units, but non-inch units are never used in practice. The system would also work if N were non-integral, and indeed Jarno (Beale) proposed at least a No. 2 1/2.)

The distance you go longitudinally along the taper is 5 times this. But (5 * N (1/10)) = N * 1/2. That is, the length of the taper section is N halves.

The big end is 25 percent larger than the small end. But eighths are 25 percent larger than tenths, so the big end is N eighths.

There you have it: For every N, a finite tapered section exists with a small end of N tenths, a big end of N eighths, and a length of N halves. It would be hard to get simpler.

1.3. Drawings and Features

Here's a drawing of Jarno tapers 6, 7, and 8 (which are about all that will fit on a regular sheet of office paper). They're drawn full-scale, but they may or may not print that way. To check, measure the Jarno No. 8 taper; it should be 4 inches long, 1 inch on the big end, and 0.8 inches on the small end.

Here's another, and rather more thorough, Jarno taper study. It shows all integral tapers from No. 1 to No. 24, plus fractional tapers Nos. 2 1/2 and 3 1/2. It also shows the progression of the large end diameters and small end diameters. It was drawn full-scale with N in inches (but of course would scale linearly were N in any other units). Full-scale, this drawing is 62 inches wide and 110 inches tall (plus margins, if any), so you probably don't want to try to print it. It's a bit obsessive, but sometimes obsessiveness can be useful.

Here's the DXF source:

• crd-10-jarno-taper-study-temp-subset.dxf
• crd-10-jarno-taper-study.dxf

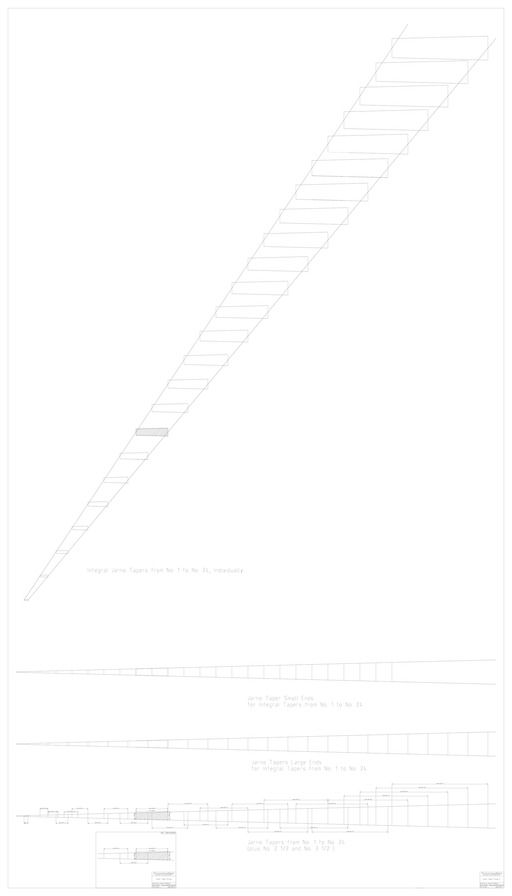
It is apparent that under Jarno No. 4 there are portions which are covered by no integrally numbered Jarno taper, and that from Jarno No. 6 on the tapers overlap. This overlap becomes quite pronounced as the series increases.

It is also interesting to observe that the small end diameters increase regularly on 2-inch intervals down the overall taper, and the large diameters do the same on 2 1/2 inch intervals (25 percent larger).

Generally modern tables seem to list Jarno tapers from 2 to 20, but Jarno (Beale) himself mentions tapers through 24 as well as half-integral tapers. For his discussion of preferred sizes (and also for the tang or tenon in Jarno taper tooling) see American Machinist for Nov. 28, 1889 , below.

2. History

In the 19th and 20th centuries (and, rarely, still) it was common for authors to write for technical publication under clearly assumed pen names. "Jarno" was the pen name of Oscar J. Beale, who in real life was basically the head of engineering at Brown & Sharpe in the late 19th century (when their development of precision metrology was at a high point).

Writing as "Jarno" in The American Machinist, Beale introduced this taper in a series of articles in 1889 discussing tapers and the problems of having too many incompatible and proprietery standards. (Note: In the series of extracts below, I have omitted various letters in reply to Jarno's articles; generally they are simply affirmative and contribute little.)

3. Usage

According to the www.lathes.co.uk site (a comprehensive reference), the Monarch 10EE toolroom lathe employed a Jarno No. 12 taper in its headstock.

Whether a machine with a 1:20 taper whose manufacturers never said that it used a Jarno taper and whose taper isn't any full-length integral or half-integral Jarno numbered taper has a "Jarno" taper is a matter of opinion and definition. Jarno (Beale) would have said that it does not. In American Machinist, Nov. 28, 1889 (see above), he specifically notes that such a taper should not be called by a Jarno number but rather should be identified by its small-end diameter and length.

With this caveat in mind, I'll note that my Clausing-Colchester 8014 13" lathe has in its headstock spindle a taper of 1-in-20 which could be contained within portions of a Jarno No. 15 or No. 16 taper. This lathe was made in England by Colchester and is better known by its name there, the Colchester Master 2500 (but whether the English version had the same spindle taper I do not know).