All the Linotype/Intertype machine "knows" about are the matrix's teeth. It has no awareness at all of the contents of the casting surface of the matrix, much less what might or might not be printed on the reference surface (that is, on the front side which the operator sees). However, the operator (who rarely actually counts tooth patterns) sees only the character, or more generally cares only about getting a combination of characters which will "run" in the magazines available and match the keyboards on the machines. (A particular combination of characters together with the number of matrices supplied for each constitutes a "font" of matrices.) In the end, the machine wins: it does what the tooth patterns indicate. So these sections investigate the relationship between matrix tooth combinations (as the primary organizing device), the characters cast by those matrices, and the magazine channels and keyboard keys which hold/release them.
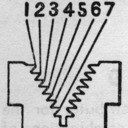
The Matrix Tooth Pattern as a Binary Number
The Linotype matrix teeth have exactly the same information capacity as an ASCII character.
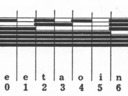
Matrix Teeth to Magazine Channel to Character
This is the basic chart which organizes all possible tooth combinations as binary numbers, and identifies the magazine channels associated with them. [PARTLY DONE:] The relationship between tooth combinations, channel numbers, and keys.

Alternative Keyboard/Magazine Layouts
[NOT DONE] (Do everything except spaces/dashes/leaders here; do them later.) [When is a Ligature not a Ligature?] [Running Fractions as Pi vs. as Keyboard.] [Advertising Figures.] [Multiple Fonts in one Keyboard.]

Examples from the Field of Inter-Font Substitution within a Magazine
[NOT DONE] Or, what it takes to keep a small, rural newspaper office running. [What does a "Font Detector" really detect?]
All portions of this document not noted otherwise are Copyright © 2008 by David M. MacMillan and Rollande Krandall.
Circuitous Root is a Registered Trademark of David M. MacMillan and Rollande Krandall.
This work is licensed under the Creative Commons "Attribution - ShareAlike" license. See http://creativecommons.org/licenses/by-sa/3.0/ for its terms.
Presented originally by Circuitous Root®
Select Resolution: 0 [other resolutions temporarily disabled due to lack of disk space]