iso
right
DMM Varkon® Tutorial
A Beginner's Guide to the Varkon
Parametric Modeling and CAD Application Development System
By David M. MacMillan
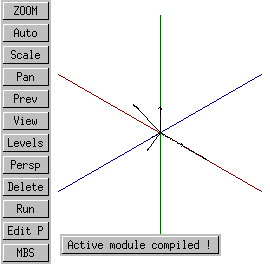
When rotating a local coordinate system with relation to another coordinate system, as you face an axis head-on, looking down the axis from the positive to the negative direction, the direction of positive rotation is counterclockwise.
The following example establishes two local coordinate systems. Each has its origin at (0, 0, 0) in the global coordinate system. One is unrotated with reference to the global coordinate system, the other is rotated 35 degrees in the positive direction around the X axis. The rotated coordinate system is made active, mostly so that it's displayed with a bigger arrow.
BASIC GEOMETRY MODULE test3d();
VECTOR neworigin1;
BEGINMODULE
part(#1,vclb(15, 0, 0));
neworigin1:=vec(0, 0, 0);
csys_1p(#2,"lcs1", neworigin1, 0, 0, 0);
csys_1p(#3,"lcs2", neworigin1, 35, 0, 0);
mode_local(#3);
ENDMODULE
 iso |
 right |
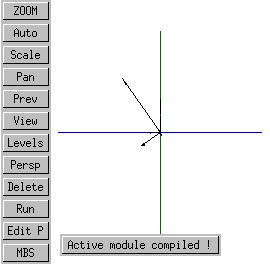
This is the equivalent rotation around the Y axis.
BASIC GEOMETRY MODULE test3d();
VECTOR neworigin1;
BEGINMODULE
part(#1,vclb(15, 0, 0));
neworigin1:=vec(0, 0, 0);
csys_1p(#2,"lcs1", neworigin1, 0, 0, 0);
csys_1p(#3,"lcs2", neworigin1, 0, 35, 0);
mode_local(#3);
ENDMODULE
 iso |
 down |
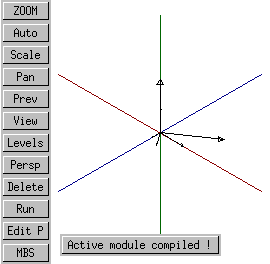
This is the equivalent rotation around the Z axis.
BASIC GEOMETRY MODULE test3d();
VECTOR neworigin1;
BEGINMODULE
part(#1,vclb(15, 0, 0));
neworigin1:=vec(0, 0, 0);
csys_1p(#2,"lcs1", neworigin1, 0, 0, 0);
csys_1p(#3,"lcs2", neworigin1, 0, 0, 35);
mode_local(#3);
ENDMODULE
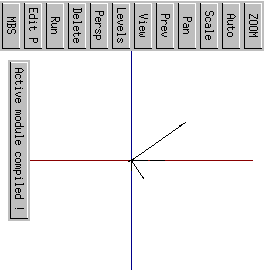
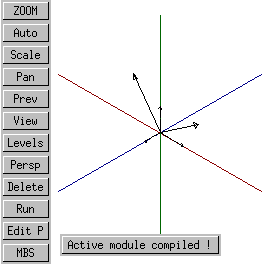 iso |
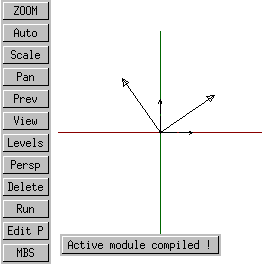 xy |
The rotation of a geometric entity is accomplished via a two-stage process. First, a transformation is defined. This transformation determines an arbitrary axis by specifying two points on that axis; it also specifies the degree of rotation around that axis. Rotation is counterclockwise when looking from the second point on the axis toward the first.
Note: There was an error in the Varkon Manual, Version 1.15 1997-10-16. In the "Copy and Transformation" section the ordering of the parameters on the tcopy() procedure is given as:
tcopy (id, transformation, entity);
The actual order is (omitting optional parameters) is:
tcopy (id, entity, transformation);
This documentation error has been corrected in version 1.16A.
In the example below, an axis is defined which runs along the X axis. It is given a direction which, for the purposes of this transformation runs from the second point (0, 0, 0) to the first point (10, 0, 0); that is, this axis points from negative to positive. Since the rotation is specified as a positive number, and rotation is counterclockwise looking from point 2 to point 1, this means that this transformation defines a rotation opposite that ordinary for the X axis.
BASIC GEOMETRY MODULE test3d();
VECTOR neworigin1;
BEGINMODULE
part(#1,vclb(15, 0, 0));
neworigin1:=vec(0, 0, 0);
csys_1p(#2,"lcs1", neworigin1, 0, 0, 0);
part(#3,boxnorot(8, 2, 4, 0, 0, 0),#2);
tform_rotl(#4,vec(10, 0, 0), vec(0, 0, 0), 45);
tcopy(#5,#3, #4);
tcopy(#6,#5, #4);
tcopy(#7,#6, #4);
ENDMODULE
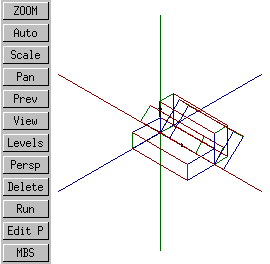 iso |
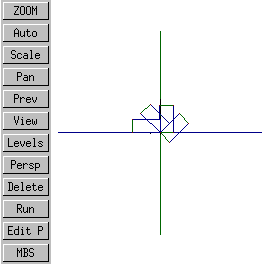 right |
By reversing the direction of the rotational transformation's axis, so that it points from positive to negative, the direction of rotation can be reversed.
tform_rotl(#4,vec(0, 0, 0), vec(10, 0, 0), 45);
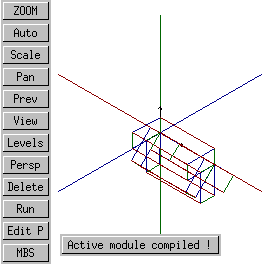 iso |
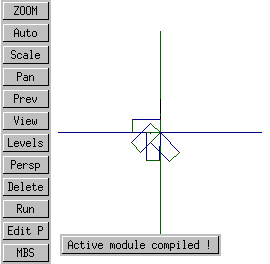 right |
With the exception of any material noted as being in the public domain, the text, images, and encoding of this document are copyright © 1998 by David M. MacMillan.
The author has no relationship with Microform AB, and this Tutorial is neither a product of nor endorsed by Microform AB.
"Varkon" is a registered trademark of Microform AB, Sweden.
This document is licensed for private, noncommercial, nonprofit viewing by individuals on the World Wide Web. Any other use or copying, including but not limited to republication in printed or electronic media, modification or the creation of derivative works, and any use for profit, is prohibited.
This writing is distributed in the hope that it will be useful, but "as-is," without any warranty of any kind, expressed or implied; without even the implied warranty of merchantability or fitness for a particular purpose.
In no event will the author(s) or editor(s) of this document be liable to you or to any other party for damages, including any general, special, incidental or consequential damages arising out of your use of or inability to use this document or the information contained in it, even if you have been advised of the possibility of such damages.
In no event will the author(s) or editor(s) of this document be liable to you or to any other party for any injury, death, disfigurement, or other personal damage arising out of your use of or inability to use this document or the information contained in it, even if you have been advised of the possibility of such injury, death, disfigurement, or other personal damage.
All trademarks or registered trademarks used in this document are the properties of their respective owners and (with the possible exception of any marks owned by the author(s) or editor(s) of this document) are used here for purposes of identification only. A trademark catalog page lists the marks known to be used on these web pages. Please e-mail dmm@lemur.com if you believe that the recognition of a trademark has been overlooked.
Version
1.3, 1998/06/17.
Feedback to dmm@lemur.com
http://www.database.com/~lemur/vk-coordrot.html
Go to the: