DMM Varkon^® Tutorial
A Beginner's Guide to the Varkon Parametric Modeling and CAD Application Development System
By David M. MacMillan

5. Coordinate Systems

1. Visualizing a Coordinate System
2. Establishing a Local Coordinate System
3. Direction of Rotation
4. Orientation of Geometric Entities
5. Summary: Local, Global, Basic

5.1. Visualizing a Coordinate System

Varkon coordinate systems are two or three dimensional Cartesian systems consisting of an X, a Y, and, if the coordinate system is three-dimensional, a Z axis. Three-dimensional coordinate systems are "right-handed." (See the Geometry Center's Geometry Formulas and Facts for an explanation of right-handedness in 3D coordinate systems.) The origin of any coordinate system is a (0, 0, 0) for that system.

Since the Varkon system imposes no fixed set of views on the model (as some CAD systems do by laying out "first projection" or "third projection" viewing arrangements), it does not in general make sense to say that a particular axis is in a particular orientation relative to the screen. However, it is useful to see how an unrotated coordinate system appears in each of the standard "8 views" available in a default Varkon user interface.

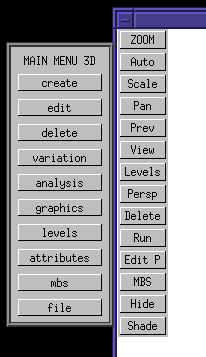
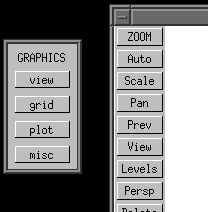
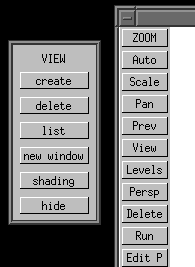
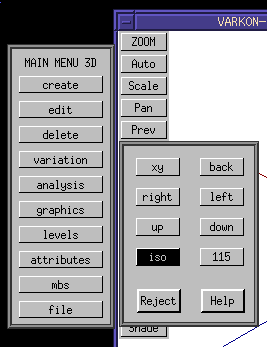
To enable these "8 views" using the standard Varkon menus, first go to the "MAIN MENU 3D". Then click on the "graphics" button. This brings up the "GRAPHICS" menu. Then click on the "view" button. This brings up the "VIEW" menu.

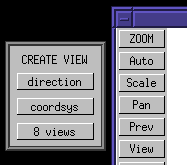
Then click on the "create" button. This brings up the "CREATE VIEW" menu. Finally, within the "CREATE VIEW" menu click on "8 views." Nothing will appear to happen. Use the right mouse button to return out of this nest of menu clicks.

Back at the drawing window, click on the "View" button.

This displays the eight available views. For now, click on the "iso" view (which stands for ISOmetric, not the International Organziation for Standardization).

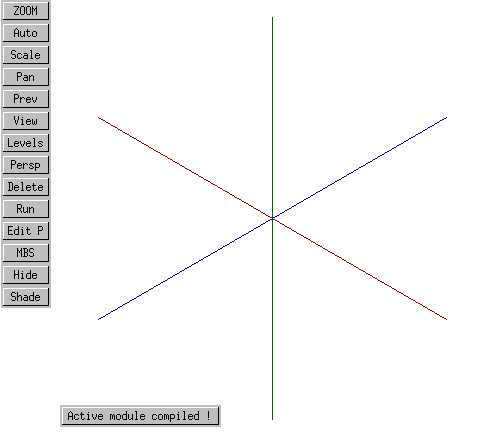
To visualize the coordinate system, we'll use the MBS module defined below. This is a GLOBAL module, so it uses whatever the current global coordinate system is (more on that later). It draws three lines, one for each axis. Red is used for the X axis, Green for the Y, and Blue for the Z. There is no good reason for this coloring, other than the fact that "RGB" is in the same order as "XYZ." (Unfortunately, text is not available in 3D Geometry mode, so we can't simply label these axes.)

! vcl.mbs Visible Coordinate Lines
!
! Draw 3 axes to illustrate a coordinate system
!
! X = red, Y = green, Z = blue
! (because I'm used to "RGB" in that order and "XYZ" in that order)

global geometry module vcl(
float delta; ! half-width of the axis line
float axisthickness; ! thickness of the axis lines
int linetype ! LFONT
);

vector xstart, xstop;
vector ystart, ystop;
vector zstart, zstop;

beginmodule

mode_basic (); ! probably redundant; force to BASIC coordinate system

! draw a visible X axis from negative to positive
xstart := vec (-delta, 0, 0);
xstop := vec ( delta, 0, 0);
lin_free(#1, xstart, xstop: PEN=2, WIDTH=axisthickness, LFONT=linetype);

! draw a visible Y axis from negative to positive
ystart := vec (0, -delta, 0);
ystop := vec (0, delta, 0);
lin_free(#2, ystart, ystop: PEN=3, WIDTH=axisthickness, LFONT=linetype);

! draw a visible Z axis from negative to positive
zstart := vec (0, 0, -delta);
zstop := vec (0, 0, delta);
lin_free(#3, zstart, zstop:PEN=4, WIDTH=axisthickness, LFONT=linetype);

endmodule

Using this vcl module, we can write an active module which calls it:

BASIC GEOMETRY MODULE test3d();
BEGINMODULE
part(#1,vclb(15, 0, 1));
ENDMODULE

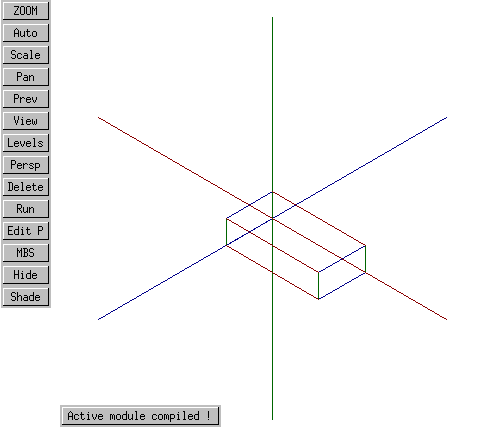
X is red, Y is green, Z is blue. Still, it's not clear which directions are positive and negative on these axes (does Z, for instance, go "in" or "out"?) To make this clear, let's use the MBS routine below to draw a box in the first quadrant. All points within this box are greater than or equal to zero.

! box1q.MBS
!
! Draw a box in the first quadrant
!
! Use the same coloring for the lines defining the box as is used for
! demonstration axes in vcl.MBS:
! X = red, Y = green, Z = blue (RGB == XYZ)
!

global geometry module box1q(
float x;
float y;
float z
);

vector lbb; ! left back bottom; origin
vector lbt; ! left back top
vector lft; ! left front top
vector lfb; ! left front bottom

vector rbb; ! right back bottom
vector rbt; ! right back top
vector rft; ! right front top
vector rfb; ! right front bottom

beginmodule

lbb := vec (0, 0, 0);
lbt := vec (0, y, 0);
lft := vec (0, y, z);
lfb := vec (0, 0, z);

lin_free (#1, lfb, lbb: PEN=4);
lin_free (#2, lft, lbt: PEN=4);
lin_free (#3, lfb, lft: PEN=3);
lin_free (#4, lbb, lbt: PEN=3);

rbb := vec (x, 0, 0);
rbt := vec (x, y, 0);
rft := vec (x, y, z);
rfb := vec (x, 0, z);

lin_free (#5, rfb, rbb: PEN=4);
lin_free (#6, rft, rbt: PEN=4);
lin_free (#7, rfb, rft: PEN=3);
lin_free (#8, rbb, rbt: PEN=3);

lin_free (#9, lbb, rbb: PEN=2);
lin_free (#10, lfb, rfb: PEN=2);

lin_free (#11, lbt, rbt: PEN=2);
lin_free (#12, lft, rft: PEN=2);

endmodule

We can instantiate this first-quadrant box by modifying the active module so that it contains the following:

BASIC GEOMETRY MODULE test3d();
BEGINMODULE
part(#1,vclb(15, 0, 1));
part(#2,box1q(8, 2, 4));
ENDMODULE

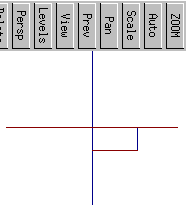	down(from above)
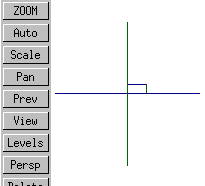left	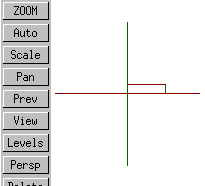xy	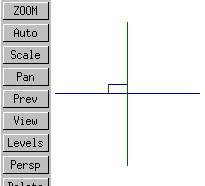right
	up (from below)
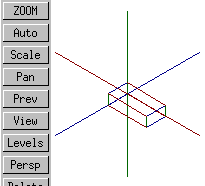isometric	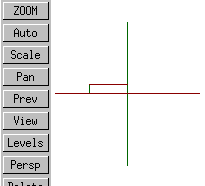back	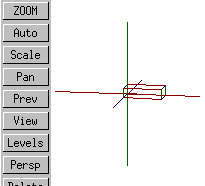115

The short of it is that in Varkon's isometric projection X increases to the right, Y increases up, and Z points more or less out of the screen.

Legal Matters

Version 1.5, 1998/06/17. Feedback to dmm@lemur.com
http://www.database.com/~lemur/vk-coordvis.html

Go to the:

• DMM Varkon Tutorial - 5.2. Establishing a Local Coordinate System
• DMM Varkon Tutorial - 4.5. Editing and Compiling MBS Code
• DMM Varkon Tutorial - 1. Main Page and Contents
• Official Varkon Homepage

• Delightful Machines Page
• Singing Lemur ^TM Home Page